(a) The differential equation is separable, so we separate the variables and integrate:
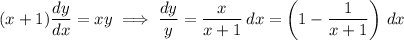
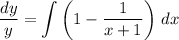

When x = 0, we have y = 2, so we solve for the constant C :
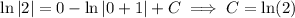
Then the particular solution to the DE is
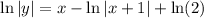
We can go on to solve explicitly for y in terms of x :
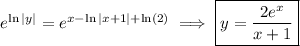
(b) The curves y = x² and y = 2x - x² intersect for
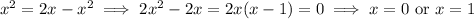
and the bounded region is the set
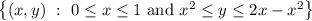
The area of this region is
