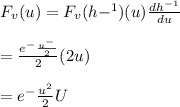Question

In a missile-testing program, one random variable of interest is the distance between the point at which the missile lands and the center of the target at which the missile was aimed. If we think of the center of the target as the origin of a coordinate system, we can let Y1 denote the northsouth distance between the landing point and the target center and let Y2 denote the corresponding eastwest distance. (Assume that north and east define positive directions.) The distance between the landing point and the target center is then U=sqrt((y1)^2+(y2)^2). If Y1 and Y2 are independent, standard normal random variables, find the probability density function

Answer 1

Explanation:

From the given data

we observed that the missile testing program

Y1 and Y2 are variable, they are also independent

We are aware that

`(Y_1)^2 and (Y_2)^2` have
`x^2` distribution with 1 degree of freedom

and
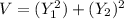`V=(Y_1^2)+(Y_2)^2` has x^2 with 2 degree of freedom

`F_v(v)=\frac{e^{-(v)/(2)}}2`

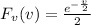
Since we have to find the density formula

`U=√(V)`

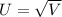
We use method of transformation

`h(V)=√(U)\\\\=U`

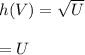
There inverse function is
`h^-^1(U)=U^2`

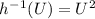
We derivate the fuction above with respect to u

`(d)/(du) (h^-^1(u))=(d)/(du) (u^2)\\\\=2u^2^-^1\\\\=2u`

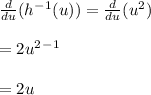
Therefore,

`F_v(u)=F_v(h-^1)(u)(dh^-^1)/(du) \\\\=(e^-(u^-^)/(2) )/(2) (2u)\\\\=e^-{(u^2)/(2) }U`