Answer:
(1) 4.09% of the New York City commutes are for less than 26 minutes.
(2) 14.32% are between 26 and 32 minutes.
(3) 54.23% are between 26 and 40 minutes.
Explanation:
We are given that the longest one-way travel time is in New York City, where the mean time is 38.5 minutes.
Assume the distribution of travel times in New York City follows the normal probability distribution and the standard deviation is 7.2 minutes.
Let X = travel times in New York City.
So, X ~ Normal(
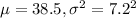 )
)
The z-score probability distribution for the normal distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = population mean travel time = 38.5 minutes
= population mean travel time = 38.5 minutes
 = standard deviation = 7.2 minutes
= standard deviation = 7.2 minutes
(1) The percent of the New York City commutes that are less than 26 minutes is given by = P(X < 26 minutes)
P(X < 26 minutes) = P(
 <
<
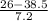 ) = P(Z < -1.74) = 1 - P(Z
) = P(Z < -1.74) = 1 - P(Z
 1.74)
1.74)
= 1 - 0.9591 = 0.0409 = 4.09%
The above probability is calculated by looking at the value of x = 1.74 in the z table which has an area of 0.9591.
(2) The percent of the New York City commutes that are between 26 and 32 minutes is given by = P(26 min < X < 32 min) = P(X < 32 min) - P(X
 26 min)
26 min)
P(X < 32 min) = P(
 <
<
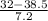 ) = P(Z < -0.90) = 1 - P(Z
) = P(Z < -0.90) = 1 - P(Z
 0.90)
0.90)
= 1 - 0.8159 = 0.1841
P(X
 26 min) = P(
26 min) = P(


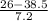 ) = P(Z
) = P(Z
 -1.74) = 1 - P(Z < 1.74)
-1.74) = 1 - P(Z < 1.74)
= 1 - 0.9591 = 0.0409
The above probability is calculated by looking at the value of x = 0.90 and x = 1.74 in the z table which has an area of 0.8159 and 0.881 respectively.
Therefore, P(26 min < X < 32 min) = 0.1841 - 0.0409 = 0.1432 or 14.32%.
(3) The percent of the New York City commutes that are between 26 and 40 minutes is given by = P(26 min < X < 40 min) = P(X < 40 min) - P(X
 26 min)
26 min)
P(X < 40 min) = P(
 <
<
 ) = P(Z < 0.21) = 0.5832
) = P(Z < 0.21) = 0.5832
P(X
 26 min) = P(
26 min) = P(


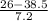 ) = P(Z
) = P(Z
 -1.74) = 1 - P(Z < 1.74)
-1.74) = 1 - P(Z < 1.74)
= 1 - 0.9591 = 0.0409
The above probability is calculated by looking at the value of x = 0.21 and x = 1.74 in the z table which has an area of 0.5832 and 0.881 respectively.
Therefore, P(26 min < X < 40 min) = 0.5832 - 0.0409 = 0.5423 or 54.23%