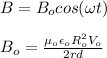Question

Suppose that a circular parallel-plate capacitor has radius R0 = 3.0 cm and plate separation d = 5.0 mm. A sinusoidal potential difference V = V0 sin(2πft) is applied across the plates, where V0 = 150 V and f = 60 Hz. In the region between the plates, find the magnitude of the induced magnetic field versus R and t, where R is the radial distance from the capacitor’s central axis. Assume that B = B0(R) is the amplitude of the magnetic field.

Answer 1

`B=(\mu_o \epsilon_o R_o^2V_o)/(2rd)cos(\omega t)`

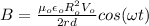
Step-by-step explanation:

By the information of the statement you have that the sinusoidal potential difference is given by:

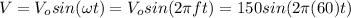`V=V_osin(\omega t)=V_osin(2\pi ft)=150sin(2\pi (60)t)` (1)

In order to calculate the induced magnetic field in between the plates, you first take into account the following formula, which is the Ampere-Maxwell law:

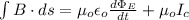`\int B\cdot ds=\mu_o \epsilon_o(d\Phi_E)/(dt)+\mu_oI_c` (2)

B: induced magnetic field

μo: magnetic permeability of vacuum = 4π*10^-7 A/T

εo: dielectric permittivity of vacuum = 8.85*10^-12 C^2/Nm^2

Ic: conduction current

ФE: electric flux

There is no conduction current in between the plates, then Ic = 0A

Next, you calculate dФE/dt, as follow:

The electric field, and the electric flux, are:

`E=(V)/(d)=(V_osin(\omega t))/(d)\\\\\Phi_E=EA`

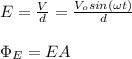
d: separation between plates = 5.0mm = 5.0*10^-3 m

A: area of the circular plates =
`\pi R_o^2`

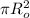
Ro: radius of the circular capacitor = 3.0cm = 0.03m

Thus, dФE/dt is:

`(d\Phi_E)/(dt)=(d(EA))/(dt)=\pi R_o^2(d)/(dt)[(V_osin(\omega t))/(d)]\\\\(d\Phi_E)/(dt)=(\pi \omega R_o^2 V_o)/(d)cos(\omega t)` (3)

The induced magnetic field is calculated by taking into account that the integral of the equation (2) is:

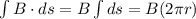`\int B \cdot ds=B\int ds=B(2\pi r)` (4)

Next, you replace the results of (3) and (4) into the equation (2) and you solve for B:

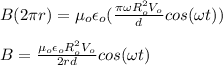`B(2\pi r)=\mu_o \epsilon_o ((\pi \omega R_o^2 V_o)/(d)cos(\omega t))\\\\B=(\mu_o \epsilon_o R_o^2V_o)/(2rd)cos(\omega t)` (5)

The last expression is de induced magnetic field in between the plates in terms of t and r

Another way of expressing the formula (5) is as follow:

`B=B_ocos(\omega t)\\\\B_o=(\mu_o \epsilon_o R_o^2V_o)/(2rd)`