Question

Exposure to microbial products, especially endotoxin, may have an impact on vulnerability to allergic diseases. The following are data on concentration (EU/mg) in settled dust for one sample of urban homes and another of farm homes.

U: 6.0 5.0 11.0 33.0 4.0 5.0 80.0 18.0 35.0 17.0 23.0
F: 2.0 15.0 12.0 8.0 8.0 7.0 6.0 19.0 3.0 9.8 22.0 9.6 2.0 2.0 0.5
A. Determine the sample mean for each sample.
B. Determine the sample median for each sample.
C. Calculate the trimmed mean for each sample by deleting the smallest and largest observation.
D. What are the corresponding trimming percentages?

Answer 1

A. E ( U ) = 21.5454 , E ( F ) = 8.39333

B. M ( U ) = 17.0 , M ( F ) = 18.0

C. E ( U' ) = 17.0 , E ( F' ) = 7.95384

D. T ( U ) = 9.091% , T ( F ) = 6.667%

Explanation:

Solution:-

- Two sample sets ( U ) and ( F ) that define the concentration ( EU/mg ) of endotoxin found in urban and farm homes as follows:

U: 6.0 5.0 11.0 33.0 4.0 5.0 80.0 18.0 35.0 17.0 23.0

F: 2.0 15.0 12.0 8.0 8.0 7.0 6.0 19.0 3.0 9.8 22.0 9.6 2.0 2.0 0.5

- To determine the mean of a sample E ( U ) or E ( F ) the following formula from descriptive statistics is used:

`E ( X ) = Sum ( X_i ) / n`

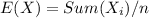
Where,

Xi : Data iteration

n: Sample size

Therefore,

`E ( U ) = (Sum (U_i ))/(n_u) \\\\E ( U ) = (6.0 + 5.0 + 11.0 + 33.0 + 4.0+ 5.0 +80.0+ 18.0+ 35.0+ 17.0+ 23.0 )/(11) \\\\E ( U ) = 21.54545\\\\E ( F ) = (Sum (F_i ))/(n_f) \\\\E ( F ) = (2.0 + 15.0 + 12.0 + 8.0 + 8.0 + 7.0 + 6.0 + 19.0+ 3.0+ 9.8+ 22.0+ 9.6+ 2.0+ 2.0+ 0.5 )/(15) \\\\E ( F ) = 8.39333`

- To determine the sample median we need to arrange the data for both samples ( U ) and ( F ) in ascending order as follows:

U: 4.0 5.0 5.0 6.0 11.0 17.0 18.0 23.0 33.0 35.0 80.0

F: 0.5 2.0 2.0 2.0 3.0 6.0 7.0 8.0 8.0 9.6 9.8 12.0 15.0 19.0 22.0

- Now find the mid value for both sets:

Median term ( U ) = ( n + 1 ) / 2

= ( 11 + 1 ) / 2 = 12/2 = 6th term

Median ( U ), 6th term = 17.0

Median term ( F ) = ( n + 1 ) / 2

= ( 15 + 1 ) / 2 = 16/2 = 8th term

Median ( F ), 8th term = 8.0

- We will now trim the smallest and largest observation from each set.

- In set ( U ) we see that smallest data corresponds to ( 4.0 ) while the largest data corresponds to ( 80.0 ). We will exclude these two terms and the trimmed set is defined as:

U': 5.0 5.0 6.0 11.0 17.0 18.0 23.0 33.0 35.0

- In set ( F ) we see that the smallest data corresponds to ( 0.5 ) while the largest data corresponds to ( 22.0 ). We will exclude these two terms and the trimmed set is defined as:

F': 2.0 15.0 12.0 8.0 8.0 7.0 6.0 19.0 3.0 9.8 9.6 2.0 2.0

- We will again use the previous formula to calculate means of trimmed samples ( U' ) and ( F' ) as follows:

`E ( U' ) = (5.0+ 5.0+ 6.0+ 11.0+ 17.0+ 18.0+ 23.0+ 33.0+ 35.0)/(9) \\\\E ( U' ) = 17`

`E ( F' ) = (2.0 +2.0+ 2.0 +3.0+ 6.0+ 7.0+ 8.0+ 8.0+ 9.6+ 9.8+ 12.0+ 15.0+ 19.0)/(13) \\\\E ( F' ) = 7.95384`

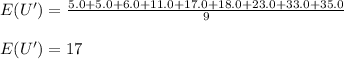
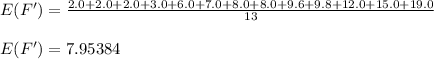
- The trimming percentage is known as the amount of data removed from the original sample from top and bottom of sample size of 11 and 15, respectively.

- We removed the smallest and largest value from each set. Hence, a single value was removed from both top and bottom of each data set. We can express the trimming percentage for each set as follows:

`T ( U ) = (1)/(11) * 100 = 9.091\\\\T ( F ) = (1)/(15) * 100 = 6.667`%

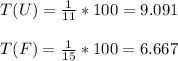- The trimming pecentages for each data set are 9.091% and 6.667% respectively.