Question

The contents of a sample of 26 cans of beer showed a standard deviation of 0.06 ounce. We are interested in testing to determine whether the variance of the population is significantly more than .003. The null hypothesis is:______.

a. should be rejected.
b. should be revised.
c. should not be rejected.
d. none of these answer.

Answer 1

The null hypothesis should not be rejected.

Explanation:

We are given that the contents of a sample of 26 cans of beer showed a standard deviation of 0.06 ounce.

Let
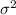`\sigma^(2)` = population variance

So, Null Hypothesis,
`H_0` :
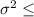`\sigma^(2) \leq` 0.003 {means that the variance of the population is significantly less than or equal to 0.003}

Alternate Hypothesis,
`H_A` :
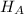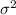`\sigma^(2)` > 0.003 {means that the variance of the population is significantly more than 0.003}

The test statistics that would be used here One-sample chi-square test statistics;

T.S. =
`((n-1)* s^(2) )/(\sigma^(2) )` ~
`\chi^(2)__n_-_1`

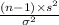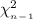
where,
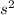`s^(2)` = sample variance =
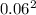`0.06^(2)` = 0.0036 ounces

n = sample of cans of beer = 26

So, the test statistics =
`((26-1)* 0.0036 )/(0.003 )` ~
`\chi^(2)__2_5`

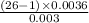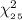
= 30

The value of chi-square test statistics is 30.

Since in the question, we are not given with the level of significance so we assume it to be 5%. Now at 5% level of significance, the ch-square table gives a critical value of 37.65 for right-tailed test.

Since our test statistics is less than the critical value of chi as 30 < 37.65, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region.

Therefore, we conclude that the variance of the population is significantly less than or equal to 0.003.