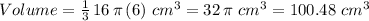Question

Need help ASAP thankyou!!!!

Answer 1

Volume =
`100.48 \,\,cm^3`

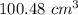
Explanation:

Recall that the volume of the cone is given by the formula:

`Volume=(1)/(3) Base * Height`

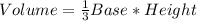
that is, one third of the product of the triangles base area times the triangle's height. In this case, the area of the base is a circle of radius 4 cm which using the formula for the area of the circle gives:

`\pi\,R^2=\pi\,(4\,\.cm)^2=16\,\pi\,\,cm^2`

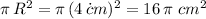
using this expression for the base in the volume formula, as well as the height of the cone (6 cm) it renders:

`Volume=(1)/(3) \,16\,\pi\,(6)\,\,cm^3=32\,\pi\,\, cm^3=100.48 \,\,cm^3`

Answer 2

V =100.48 cm^3

Explanation:

The volume of a cone is given by

V = 1/3 pi r^2 h

V = 1/3 pi ( 4)^2 6

V = 1/3 pi ( 16)*6

V =32 pi cm^3

Let pi 3.14

V =100.48 cm^3