Answer:
(a) The probability that the thickness is less than 3.0 mm is 0.119.
(b) The probability that the thickness is more than 7.0 mm is 0.119.
(c) The probability that the thickness is between 3.0 mm and 7.0 mm is 0.762.
Explanation:
We are given that thickness measurements of ancient prehistoric Native American pot shards discovered in a Hopi village are approximately normally distributed, with a mean of 5.0 millimeters (mm) and a standard deviation of 1.7 mm.
Let X = thickness measurements of ancient prehistoric Native American pot shards discovered in a Hopi village.
So, X ~ Normal(
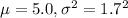 )
)
The z-score probability distribution for the normal distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = population mean thickness = 5.0 mm
= population mean thickness = 5.0 mm
 = standard deviation = 1.7 mm
= standard deviation = 1.7 mm
(a) The probability that the thickness is less than 3.0 mm is given by = P(X < 3.0 mm)
P(X < 3.0 mm) = P(
 <
<
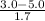 ) = P(Z < -1.18) = 1 - P(Z
) = P(Z < -1.18) = 1 - P(Z
 1.18)
1.18)
= 1 - 0.8810 = 0.119
The above probability is calculated by looking at the value of x = 1.18 in the z table which has an area of 0.881.
(b) The probability that the thickness is more than 7.0 mm is given by = P(X > 7.0 mm)
P(X > 7.0 mm) = P(
 >
>
 ) = P(Z > 1.18) = 1 - P(Z
) = P(Z > 1.18) = 1 - P(Z
 1.18)
1.18)
= 1 - 0.8810 = 0.119
The above probability is calculated by looking at the value of x = 1.18 in the z table which has an area of 0.881.
(c) The probability that the thickness is between 3.0 mm and 7.0 mm is given by = P(3.0 mm < X < 7.0 mm) = P(X < 7.0 mm) - P(X
 3.0 mm)
3.0 mm)
P(X < 7.0 mm) = P(
 <
<
 ) = P(Z < 1.18) = 0.881
) = P(Z < 1.18) = 0.881
P(X
 3.0 mm) = P(
3.0 mm) = P(


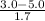 ) = P(Z
) = P(Z
 -1.18) = 1 - P(Z < 1.18)
-1.18) = 1 - P(Z < 1.18)
= 1 - 0.8810 = 0.119
The above probability is calculated by looking at the value of x = 1.18 in the z table which has an area of 0.881.
Therefore, P(3.0 mm < X < 7.0 mm) = 0.881 - 0.119 = 0.762.