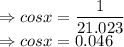Question

The value of tangent x is given. Find sine x and cos x if x lies in the specified interval.

tan x = 21​, x is an element of [0, pi / 2]

Answer 1

sin x = 0.998

cosx = 0.046

Explanation:

Given that:

tan x = 21

where interval of x is
`[0,(\pi)/(2)]`.

We know that the trigonometric identity for tan x is:

`tan\theta = (Perpendicular)/(Base)`

Comparing with:

`tan x = (21)/(1)`

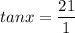
Perpendicular = 21 units

Base = 1 unit

As per pythagorean theorem:

`\text{Hypotenuse}^(2) = \text{Base}^(2) + \text{Perpendicular}^(2)\\`

`\Rightarrow \text{Hypotenuse}^2 = 21^2 +1^2\\\Rightarrow \text{Hypotenuse} = √(442) = 21.023\ units`

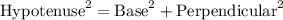
interval of x is
`[0,(\pi)/(2)]` so values of sinx and cosx will be positive because it is first quadrant where values of sine and cosine are positive.

We know that

`sin\theta = (Perpendicular)/(Hypotenuse)\\cos\theta = (Base)/(Hypotenuse)`

So, sine x :

`\Rightarrow sinx =(21)/(21.023)\\\Rightarrow sinx = 0.998`

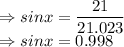
Similarly, value of cos x :

`\Rightarrow cosx =(1)/(21.023)\\\Rightarrow cosx = 0.046`