Question

Use reduction of order (NOT the integral formula we developed) to find the general solution of the nonhomogeneous linear DE, showing all work. Also clearly state the particular solution yp that you obtain using the reduction of order process and show a clear check that your particular solution yp satisfies the original nonhomogeneous DE. [Do NOT use the Method of Undetermined Coefficients here!]

''y + 6y' + 9y + 4e^x
Note: Use the characteristic polynomial to find a first solution yi of the associated homogencous DE.)

Answer 1

`y = (e^(4x){4} + kx+d) \cdot c_1e^(-3x) =  (e^(x))/(4) + Ae^(-3x)+Bxe^(-3x)` where A,B are constants.

Explanation:

Consider the differential equation
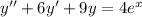`y''+6y'+9y = 4e^(x)`. To find the homogeneus solution, we assume that
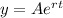`y = Ae^(rt)` and replace it in the equation
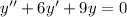`y''+6y'+9y = 0`. If we do so, after using some properties of derivatives and the properties of the exponential function we end up with the equation

`r^2+6r+9 = 0 = (r+3)^2`

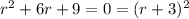
which leads to r = -3. So, one solution of the homogeneus equation is
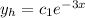`y_h = c_1e^(-3x)`, where c_1 is a constant.

To use the order reduction method, assume

`y = v(x)y_h(x)`

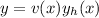
where v(x) is an appropiate function. Using this, we get

`y'= v'y+y'v`

`y''=v''y+y'v'+y''v+v'y'=v''y+2v'y'+y''v`

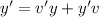
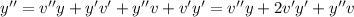
Plugging this in the original equation we get

`v''y+2v'y'+y''v + 6(v'y+y'v) +9vy=4e^(x)`

re arranging the left side we get

`v''y+2v'y'+6v'y+v(y''+6y'+9y)=4e^(x)`

Since y is a solution of the homogeneus equation, we get that
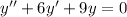`y''+6y'+9y=0`. Then we get the equation

`yv''+(2y'+6y)v' = 4e^(x)`

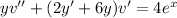
We can change the variable as w = v' and w' = v'', and replacing y with y_h, we get that the final equation to be solved is

`e^(-3x)w'+(6e^(-3x)-6e^(-3x))w =4e^(x)`

Or equivalently

`w' = 4e^(4x)`

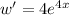
By integration on both sides, we get that w = e^{4x}+ k[/tex] where k is a constant.

So by integration we get that v =
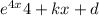`e^(4x){4} + kx+d` where d is another constant.

Then, the final solution is

`y = (e^(4x){4} + kx+d) \cdot c_1e^(-3x) =  (e^(x))/(4) + Ae^(-3x)+Bxe^(-3x)` where A,B are constants