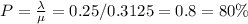Question

Wayne's service center operates a welding shop. Assume that the arrival of jobs follows a Poisson distribution with 2 jobs arriving in an 8 hour day. The time required to complete a job follows a normal distribution with a mean time of 3.2 hours and a standard deviation of 2 hours.

A. What is the mean service rate in jobs per hour?
B. What is the average number of jobs waiting for service?
C. What is the average time a job waits before the welder can begin working on it?
D. What is the average number of hours between when a job is received and when it is completed?
E. What percentage of the time is Gubser's welder busy?

Answer 1

a) 0.3125 per hour

b) 2.225 hours

c) 8.9 hours

d) 12.1 hours

e) 80%

Explanation:

Given that:

mean time = 3.2 hours, standard deviation (σ) = 2 hours

The mean service rate in jobs per hour (λ) = 2 jobs/ 8 hour = 0.25 job/hour

a) The average number of jobs waiting for service (μ)= 1/ mean time = 1/ 3.2 = 0.3125 per hour

b) The average time a job waits before the welder can begin working on it (L) is given by:

`L=(\lambda^2\sigma^2+(\lambda/\mu)^2)/(2(1-\lambda/\mu))) =(0.25^2*0.2^2+(0.25/0.3125)^2)/(2(1-0.25/0.3125))=2.225\ hours`

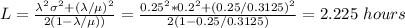
c) The average number of hours between when a job is received and when it is completed (Wq) is given as:

`W_q=(L)/(\lambda)=2.225/0.25=8.9\ hours`

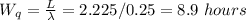
d) The average number of hours between when a job is received and when it is completed (W) is given as:

`W=W_q+(1)/(\mu) =8.9+(1)/(0.3125)=12.1 \ hours`

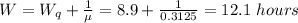
e) Percentage of the time is Gubser's welder busy (P) is given as:

`P=(\lambda)/(\mu)=0.25/0.3125=0.8=80\%`