Answer:
(27.55, 7.22), (-11.3, 3.21).
Explanation:
When is the tangent to the curve horizontal?
The tangent curve is horizontal when the derivative is zero.
The derivative is:
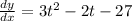
Solving a quadratic equation:
Given a second order polynomial expressed by the following equation:
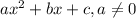 .
.
This polynomial has roots
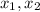 such that
such that
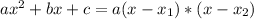 , given by the following formulas:
, given by the following formulas:
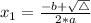
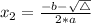

In this question:
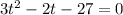
So

Then
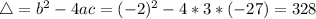
So
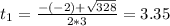
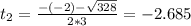
Enter your answers as a comma-separated list of ordered pairs.
We found values of t, now we have to replace in the equations for x and y.
t = 3.35
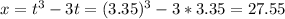
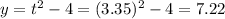
The first point is (27.55, 7.22)
t = -2.685
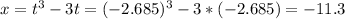

The second point is (-11.3, 3.21).