Answer:
The angle of the shaded region is 124.9°
Explanation:
Since there's an region inside the circle that is shaded and has an area of 34 pi square units, we can apply the circle's sector area's formula in order to find the angle of this region. The formula is given by:
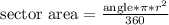
Applying the data from the problem gives us:
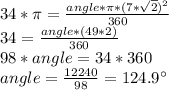
The angle of the shaded region is 124.9°