Answer:
(a) The fraction of the calls last between 4.50 and 5.30 minutes is 0.3729.
(b) The fraction of the calls last more than 5.30 minutes is 0.1271.
(c) The fraction of the calls last between 5.30 and 6.00 minutes is 0.1109.
(d) The fraction of the calls last between 4.00 and 6.00 minutes is 0.745.
(e) The time is 5.65 minutes.
Explanation:
We are given that the mean length of time per call was 4.5 minutes and the standard deviation was 0.70 minutes.
Let X = the length of the calls, in minutes.
So, X ~ Normal(
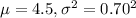 )
)
The z-score probability distribution for the normal distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = population mean time = 4.5 minutes
= population mean time = 4.5 minutes
 = standard deviation = 0.7 minutes
= standard deviation = 0.7 minutes
(a) The fraction of the calls last between 4.50 and 5.30 minutes is given by = P(4.50 min < X < 5.30 min) = P(X < 5.30 min) - P(X
 4.50 min)
4.50 min)
P(X < 5.30 min) = P(
 <
<
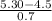 ) = P(Z < 1.14) = 0.8729
) = P(Z < 1.14) = 0.8729
P(X
 4.50 min) = P(
4.50 min) = P(


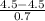 ) = P(Z
) = P(Z
 0) = 0.50
0) = 0.50
The above probability is calculated by looking at the value of x = 1.14 and x = 0 in the z table which has an area of 0.8729 and 0.50 respectively.
Therefore, P(4.50 min < X < 5.30 min) = 0.8729 - 0.50 = 0.3729.
(b) The fraction of the calls last more than 5.30 minutes is given by = P(X > 5.30 minutes)
P(X > 5.30 min) = P(
 >
>
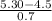 ) = P(Z > 1.14) = 1 - P(Z
) = P(Z > 1.14) = 1 - P(Z
 1.14)
1.14)
= 1 - 0.8729 = 0.1271
The above probability is calculated by looking at the value of x = 1.14 in the z table which has an area of 0.8729.
(c) The fraction of the calls last between 5.30 and 6.00 minutes is given by = P(5.30 min < X < 6.00 min) = P(X < 6.00 min) - P(X
 5.30 min)
5.30 min)
P(X < 6.00 min) = P(
 <
<
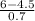 ) = P(Z < 2.14) = 0.9838
) = P(Z < 2.14) = 0.9838
P(X
 5.30 min) = P(
5.30 min) = P(


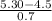 ) = P(Z
) = P(Z
 1.14) = 0.8729
1.14) = 0.8729
The above probability is calculated by looking at the value of x = 2.14 and x = 1.14 in the z table which has an area of 0.9838 and 0.8729 respectively.
Therefore, P(4.50 min < X < 5.30 min) = 0.9838 - 0.8729 = 0.1109.
(d) The fraction of the calls last between 4.00 and 6.00 minutes is given by = P(4.00 min < X < 6.00 min) = P(X < 6.00 min) - P(X
 4.00 min)
4.00 min)
P(X < 6.00 min) = P(
 <
<
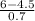 ) = P(Z < 2.14) = 0.9838
) = P(Z < 2.14) = 0.9838
P(X
 4.00 min) = P(
4.00 min) = P(


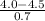 ) = P(Z
) = P(Z
 -0.71) = 1 - P(Z < 0.71)
-0.71) = 1 - P(Z < 0.71)
= 1 - 0.7612 = 0.2388
The above probability is calculated by looking at the value of x = 2.14 and x = 0.71 in the z table which has an area of 0.9838 and 0.7612 respectively.
Therefore, P(4.50 min < X < 5.30 min) = 0.9838 - 0.2388 = 0.745.
(e) We have to find the time that represents the length of the longest (in duration) 5 percent of the calls, that means;
P(X > x) = 0.05 {where x is the required time}
P(
 >
>
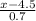 ) = 0.05
) = 0.05
P(Z >
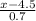 ) = 0.05
) = 0.05
Now, in the z table the critical value of x which represents the top 5% of the area is given as 1.645, that is;
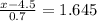
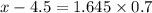
x = 4.5 + 1.15 = 5.65 minutes.
SO, the time is 5.65 minutes.