Question

The angle between vector A = 2.00i + 3.00j and vector B is 45.0°. The scalar product of vectors A 12) and B is 7.00. If the x-component of vector B is positive, what is vector B

Answer 1

B = 2.67i - 0.53j

Step-by-step explanation:

In order to find the vector B, you first take into account the following formula:

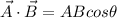`\vec{A}\cdot\vec{B}=ABcos\theta` (1)

where:

A = 2.00i + 3.00j

B = ?

θ: angle between vectors A and B = 45.0°

You use the fact that the dot product between vectors A and B is 7.00.

You calculate the magnitude of A vector as follow:

`A=√((2.00)^2+(3.00)^2)=3.60`

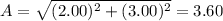
Then, you solve the equation (1) for the magnitude of B:

`B=\frac{\vec{A}\cdot\vec{B}}{Acos\theta}=(7.00)/(3.60cos(45\°))=2.74`

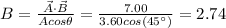
Next, you can consider that the A vector is the x axis of the coordinate system, to calculate the components of B. This means that the coordinate system is rotated an angle equivalent to the angle of A respect to the x axis.

With the previous assumption you have that the components of B are:

`B_x=Bcos\theta=(2.74)cos45\°=1.93\\\\B_y=Bsin45\°=(2.74)sin45\°=1.93`

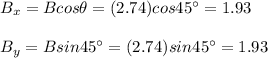
The vector B is:

B = 1.93i + 1.93j

Next, it is necessary to rotate again the coordinate system to its original position. For that, you calculate the angle of A:

`\alpha=tan^(-1)((3.00)/(2.00))=56.30`

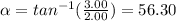
In order to calculate the real components of B, you rotate the system 56.30°, by using the following relation:

`B_x'=B_xcos\alpha+B_ysin\alpha\\\\B_x'=1.93cos(56.30\°)+1.93sin(56.30\°)=2.67\\\\B_y'=-B_xsin\alpha+B_ycos\alpha\\\\B_y'=-1.93sin(56.30\°)+1.93cos(56.30\°)=-0.53`

The vector B is:

B = 2.67i - 0.53j