Question

Two geekie physics students with a combined mass of 136 kg jump into their old car to run out for some late night pizza. The distance between the front and back axles of the car is 2.9 m. When they get in the car, the springs compress a total of 8.2 cm. On their way to the Pizza Hut, when they go over a bump, the car oscillates up and down with a period of 1.7 seconds.

What is mass of the car?
mcar =

Answer 1

1052.5 kg

Step-by-step explanation:

The mass of the car can be calculated as follows:

`\omega = \sqrt{(k)/(M)}`

Where:

ω: is the angular speed

k: is the spring constant

M: is the combined mass of the car and the students

The angular speed is:

`\omega = (2\pi)/(T)`

Where T is the period

`\omega = (2\pi)/(1.7 s) = 3.7 rad/s`

Now, the spring constant is:

`F = mg`

`kx = mg`

`k = (mg)/(x)`

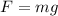
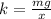
Where:

m: is the mass of the students = 136 kg

x: is the disntace at which the spring compress = 8.2 cm = 0.082 m

`k = (136 kg*9.81 m/s^(2))/(0.082 m) = 16270.2 N/m`

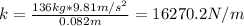
Finally, we can find the mass of the car:

`M = (k)/(\omega^(2)) = (16270.2 N/m)/((3.7 rad/s)^(2)) = 1188.5 kg`

`m_(c) = M - m = 1188.5 kg - 136 kg = 1052.5 kg`

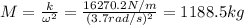
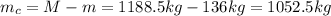
Hence, the mass of the car is 1052.5 kg.

I hope it helps you!