Answer:
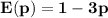
the estimate the percent change in q when the price is raised from $2.00 to $2.10 decreases by 25%
Explanation:
Given that:
the number of units demanded
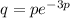
Taking differentiations ; we have,

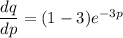
Now; the price elasticity of demand using the differentials definition of elasticity is:
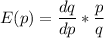
![E(p) =[(1-3)e^(-3p)]*[(p)/(pe^(-3p))]](https://img.qammunity.org/2021/formulas/mathematics/college/8yc26errmzzmz56pjdh5zvvbdmu6bakui4.png)
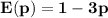
(b) Use your answer from part (a) to estimate the percent change in q when the price is raised from $2.00 to $2.10.
The estimate of the percentage change in price is :
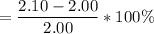
= 5%
From (a)
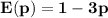
Now at p = $2.00
E(2) = 1 - 3 (2.00)
E(2) = 1 - 6
E(2) = -5
The percentage change in q = -5 × 5%
The percentage change in q = -25%
Thus; we can conclude that the estimate the percent change in q when the price is raised from $2.00 to $2.10 decreases by 25%