Question

At which values of x does the function F(x) have a vertical asymptote? Check

all that apply,
F(x)
9
(x - 1)(x-8)

Answer 1

The correct answer is 1 and 8

Explanation:

Answer 2

The values of x that makes f(x) have a valid asymptote are 1 and 8

Explanation:

Given

`f(x) = (9)/((x-1)(x-8))`

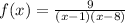
Required

At what value does f(x) has a vertical asymptote

To solve this, we simply equate the denominator of f(x) to 0;

This is done as follows

`{(x-1)(x-8)} = 0`

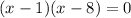
This can be split to

`{(x-1) = 0 \ or\ (x-8)} = 0`

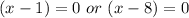
Remove brackets

`x-1 = 0 \ or\ x-8 = 0`

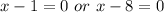
Make x the subject of formula in both cases

`x-1+1 = 0+1 \ or\ x-8+8 = 0+8`

`x= 0+1 \ or\ x = 0+8`

`x= 1 \ or\ x = 8`

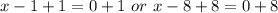
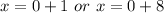
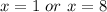
The values of x that makes f(x) have a valid asymptote are 1 and 8