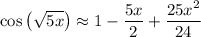Question

Find maclaurin series

Answer 1

Recall the Maclaurin expansion for cos(x), valid for all real x :

`\displaystyle \cos(x) = \sum_(n=0)^\infty (-1)^n (x^(2n))/((2n)!)`

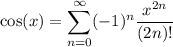
Then replacing x with √5 x (I'm assuming you mean √5 times x, and not √(5x)) gives

`\displaystyle \cos\left(\sqrt 5\,x\right) = \sum_(n=0)^\infty (-1)^n (\left(\sqrt5\,x\right)^(2n))/((2n)!) = \sum_(n=0)^\infty (-5)^n (x^(2n))/((2n)!)`

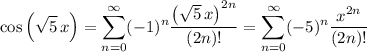
The first 3 terms of the series are

`\cos\left(\sqrt5\,x\right) \approx 1 - \frac{5x^2}2 + (25x^4)/(24)`

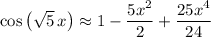
and the general n-th term is as shown in the series.

In case you did mean cos(√(5x)), we would instead end up with

`\displaystyle \cos\left(√(5x)\right) = \sum_(n=0)^\infty (-1)^n (\left(√(5x)\right)^(2n))/((2n)!) = \sum_(n=0)^\infty (-5)^n (x^n)/((2n)!)`

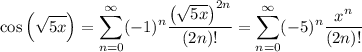
which amounts to replacing the x with √x in the expansion of cos(√5 x) :

`\cos\left(√(5x)\right) \approx 1 - \frac{5x}2 + (25x^2)/(24)`