Question

In the figure below, if m∠2=(18x+6)° and m∠3=(21x+18)° then m∠2= ____ .

Answer 1

m∠2 = 78°

Explanation:

Two lines 'l' and 'm' are parallel and another line 'n' is a transverse.

Since ∠2 and ∠3 are the consecutive interior angles,

Therefore, sum of these angles will be 180°.

m∠2 + m∠3 = 180°

(18x + 6)° + (21x + 18)° = 180°

(18x + 21x) + ( 6 + 18) = 180

39x + 24 = 180

39x = 180 - 24

39x = 156

x =
`(156)/(39)`

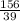
x = 4

Since, m∠2 = (18x + 6)°

By substituting the value of x = 4,

m∠2 = (18×4) + 6

= 72 + 6

= 78°

Therefore, measure of angle 2 is 78°.