The expanded form of the function f(x) is:
![\[ f(x) = x^4 - 7x^3 + 15x^2 + 41x - 50 \]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/w8xet9762uwf1z881m9tl9uvyiha2f398g.png)
This is the simplified polynomial form of the given function.
The function f(x) provided in the image is a product of four factors:
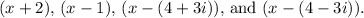 To simplify this function, we need to expand the product of these factors. Here are the steps involved:
To simplify this function, we need to expand the product of these factors. Here are the steps involved:
1. Recognize the Complex Conjugate Pair: The factors
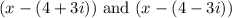 are a pair of complex conjugates. When multiplied together, they will result in a quadratic expression with real coefficients.
are a pair of complex conjugates. When multiplied together, they will result in a quadratic expression with real coefficients.
2. Multiply the Complex Conjugate Pair: We can multiply
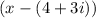 and
and
 to obtain a quadratic polynomial.
to obtain a quadratic polynomial.
3. Multiply the Remaining Real Factors: After obtaining the quadratic polynomial from the complex conjugate pair, we can then multiply it by the remaining factors (x + 2) and (x - 1) to get the expanded form of the function.
4. Expand the Entire Expression: The final step is to expand the entire expression to get f(x) in standard polynomial form.