Question

Suppose a random sample of 100 observations from a binomial population gives a value of pˆ = .63 and you wish to test the null hypothesis that the population parameter p is equal to .70 against the alternative hypothesis that p is less than .70.

a) nothing that p = .63, what does your intuition tell you? does the value of p appear to contradict the null hypothesis?
b) use the large-sample z-test to test H0: p = .70 against the alternative hypothesis, Ha: p < 70. Use a = .05. How do the test results compare with your intuitive decision from part A?
c) find and interpret the observed significance level of the test you conducted in part B.

Answer 1

We conclude that the population proportion is equal to 0.70.

Explanation:

We are given that a random sample of 100 observations from a binomial population gives a value of pˆ = 0.63 and you wish to test the null hypothesis that the population parameter p is equal to 0.70 against the alternative hypothesis that p is less than 0.70.

Let p = population proportion.

(1) The intuition tells us that the population parameter p may be less than 0.70 as the sample proportion comes out to be less than 0.70 and also the sample is large enough.

(2) So, Null Hypothesis,
`H_0` : p = 0.70 {means that the population proportion is equal to 0.70}

Alternate Hypothesis,
`H_A` : p < 0.70 {means that the population proportion is less than 0.70}

The test statistics that would be used here One-sample z-test for proportions;

T.S. =
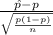`\frac{\hat p-p}{\sqrt{(p(1-p))/(n) } }` ~ N(0,1)

where,
`\hat p` = sample proportion = 0.63

n = sample of observations = 100

So, the test statistics =
`\frac{0.63-0.70}{\sqrt{(0.70(1-0.70))/(100) } }`

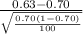
= -1.528

The value of z-test statistics is -1.528.

Now at 0.05 level of significance, the z table gives a critical value of -1.645 for the left-tailed test.

Since our test statistics is more than the critical value of z as -1.528 > -1.645, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region due to which we fail to reject our null hypothesis.

Therefore, we conclude that the population proportion is equal to 0.70.

(c) The observed level of significance in part B is 0.05 on the basis of which we find our critical value of z.