Question

You pull downward with a force of 32 N on a rope that passes over a disk-shaped pulley of mass 1.4 kg and radius 0.075 m. The other end of the rope is attached to a 0.77 kg mass.

a) Is the tension in the rope the same on both sides of the pulley? Which side has the largest tension
b) Find the tension in the rope on both sides of the pulley

Answer 1

Given::

force P = 32 N

mass of the pully M = 1.4kg

radius R = 0.075m

mass attached at the other end

=0.77kg

since the pully mass is not negligible

tensions in the rope on both sides not same

if a is the accelration of the mass m

and T₁ is the tension in the rope where the mass is attached then

ma = T₁ ₋mg1

T₁ = ma₋mg1 . . . . 1

and if T₂ the tension on the other side then

F=T₂ ..... 2

since the mass is moving up T₁ is less than T₂

So, (T₂ ₋ T₁ ) R =1 (a/R)

Putting the value of T₁ from equation 1

(T₂ ₋ ma₋mg1 ) R =1 (Ma/2)

a = (T₂ ₋ mg)/m+M/2

a =
`(32-0.77*9.8)/(0.77+1.4/2)`

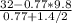
= 24.454/1.47

= 16.6353741

So, T₁ = ma₋mg

= 0.77(16.6353741+9.8)

T₁ = 20.355

T2 = 32