Question

Two planes of charge with no thickness, A and B, are paralleland vertical. The electric field in region to the left ofplane A has magnitude (3σ/2εo) and points tothe left. The electric field in the region to the right of Bhas magnitude (3σ/2εo) and points to theright. The electric field in the region between the twoplanes has magnitude (σ/2εo) and points to the right.

Find the surface charge density on planes A andB.
Does anyone know how to solve this?

Answer 1

The charge on plane A is 2σ

The charge plane B on the right is σ

Step-by-step explanation:

To solve this exercise we can use Gauss's law, to find the electric field created by each plane, let's create a cylinder-shaped Gaussian surface, where the base is parallel to the plane.

Gauss law

Ф = ∫ E. dA =
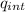`q_(int)` /ε₀

with the field it must be perpendicular to the plane and the normal one to the base of the cylinder is perpendicular, the dot product is reduced to the algebraic product.

The charge inside the cylinder

σ = q_{int} / A

q_{int} = σ A

let's replace

the flow is on both sides of the plane

2E A = σ_A /ε₀

E = σ_A / 2ε₀

Let's analyze plane A on the left, the electric field is salient so the charge must be positive

For plane B on the right we repeat the calculation, finding that the charge is positive

Now we can find the electrified field in each part

To the left of plate A

E = E_A + E_B

3σ/ 2ε₀ = σ_A/2ε₀ + σ_B / 2ε₀

3 σ = σ_A + σ_B

The electric field between the planes is the subtraction of each elective field

E = E_A -E_B

σ / 2ε₀ = σ_A / 2ε₀ - σ_B / 2ε₀

σ = σ_A -σB

Let's write our system of equations and solve

3 σ = σ_A + σ_B

σ = σ_A - σ_ B

let's add the two equations

4 σ = 2 σ_A

σ_ A = 2 σ

therefore the charge on plane A is 2σ

now let's subtract the equations

2 σ = 2 σ_B

σ_B = σ

The charge plane B on the right is σ