Question

A bottling company uses a filling machine to fill cans with an energy drink. The cans are supposed to contain 250 ml. The machine, however, has some variability, so the population standard deviation of the size is 3 ml. A sample of 6 cans is inspected each hour for process control purposes, and records are kept of the sample mean volume (x).a) Assume that the process mean is exactly equal to the target value, that is μ=250.

What will be the mean and standard deviation of the sampling distribution of the sample mean x?b) What is the probability that the volume of a single randomly chosen can differs from the target value by 1 ml or more?c) What is the probability that the sample mean volume of a random sample of 6 cans differs from the target value by 1 ml or more?

Answer 1

a) Mean 250 ml, standard deviation 1.2247 ml.

b) 74.14% probability that the volume of a single randomly chosen can differs from the target value by 1 ml or more.

c) 41.22% probability that the sample mean volume of a random sample of 6 cans differs from the target value by 1 ml or more

Explanation:

To solve this question, we need to understand the normal probability distribution and the central limit theorem.

Normal probability distribution

When the distribution is normal, we use the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

Central Limit Theorem

The Central Limit Theorem estabilishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

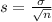For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

In this question:

`\mu = 250, \sigma = 3`

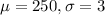
a) Assume that the process mean is exactly equal to the target value, that is μ=250. What will be the mean and standard deviation of the sampling distribution of the sample mean x?

By the Central Limit Theorem, the mean is 250 ml and the standard deviation is
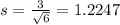`s = (3)/(√(6)) = 1.2247` ml.

b) What is the probability that the volume of a single randomly chosen can differs from the target value by 1 ml or more?

Greater than 250 + 1 = 251 or lesser than 250 - 1 = 249.

Since the normal distribution is symmetric, these probabilities are the same, so we can find one of them and multiply by 2.

Lesser than 249:

pvalue of Z when X = 249.

`Z = (X - \mu)/(\sigma)`

`Z = (249 - 250)/(3)`

`Z = -0.33`

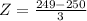
`Z = -0.33` has a pvalue of 0.3707

0.3707*0.2 = 0.7414

74.14% probability that the volume of a single randomly chosen can differs from the target value by 1 ml or more.

c) What is the probability that the sample mean volume of a random sample of 6 cans differs from the target value by 1 ml or more?

Since more than 1 can, we use the Central Limit Theorem.

The probability follows the same logic as b.

`Z = (X - \mu)/(\sigma)`

By the Central Limit Theorem

`Z = (X - \mu)/(s)`

`Z = (249 - 250)/(1.2247)`

`Z = -0.82`

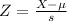
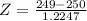
`Z = -0.82` has a pvalue of 0.2061

2*0.2061 = 0.4122

41.22% probability that the sample mean volume of a random sample of 6 cans differs from the target value by 1 ml or more