Answer:
The statement provided is TRUE.
Explanation:
The four principle assumptions of the simple linear regression model are,
- The linearity of the relationship between the dependent variable and the independent variable. That is, value of y, the dependent variable for each value of x the independent variable is,
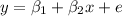 .
. - Normality of the error distribution. That is,
 . Thus, the variance of random error e is
. Thus, the variance of random error e is
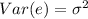 .
. - Statistical independence of the errors or specifically no correlation between consecutive errors. That is, if
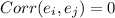 , it implies that
, it implies that
 .
. - Homoscedasticity of the errors, i.e. constant variance.
The first assumption clearly indicates that the y-values are statistically dependent upon the x-values.
Thus, the statement provided is TRUE.