Question

Assume that a procedure yields a binomial distribution with a trial repeated n times. Use the binomial probability formula to find the probability of x successes given the probability p of success on a single trial.

n=55​,
x=33​,
p=0.55
p(3)=_________

Answer 1

P(33) = 0.0826

Explanation:

The binomial distribution in this case has parameters n=55 and p=0.55.

The probability that k successes happen with these parameters can be calculated as:

`P(x=k) = \dbinom{n}{k} p^(k)(1-p)^(n-k)\\\\\\P(x=k) = \dbinom{55}{k} 0.55^(k) 0.45^(55-k)\\\\\\`

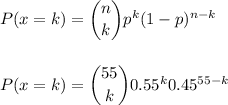
We have to calculate the probability fo X=33 succesess.

This can be calculated using the formula above as:

`P(x=33) = \dbinom{55}{33} p^(33)(1-p)^(22)\\\\\\P(x=33) =1300853625660220*0.0000000027*0.0000000235\\\\\\P(x=33) =0.0826\\\\\\`