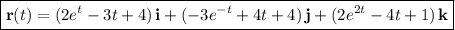Integrating both sides once gives
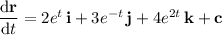
where
 is an arbitrary constant vector. Use the initial condition to find its value:
is an arbitrary constant vector. Use the initial condition to find its value:
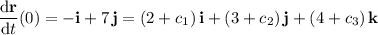
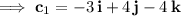
Integrate again:
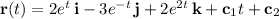
where
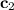 is another arbitrary vector of constants. Use the other initial condition to determine its components:
is another arbitrary vector of constants. Use the other initial condition to determine its components:
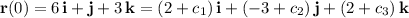
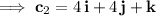
Then the particular solution to this ODE is