Question

The number of customers waiting for gift-wrap service at a department store is an rv X with possible values 0, 1, 2, 3, 4 and corresponding probabilities 0.1, 0.2, 0.3, 0.25, 0.15. A randomly selected customer will have 1, 2, or 3 packages for wrapping with probabilities 0.55, 0.35, and 0.1, respectively. Let Y = the total number of packages to be wrapped for the customers waiting in line (assume that the number of packages submitted by one customer is independent of the number submitted by any other customer).

(a) Determine P(X = 3, Y = 3), i.e., p(3,3). (Round your answer to four decimal places.)
(b) Determine p(4,11). (Round your answer to four decimal places.) p(4,11) = ?

Answer 1

(a)p(3,3)=0.0416

(b)p(4,11)=0.0002

Explanation:

Number of Customers, X

`\left\begin{array}cccccX&0&1&2&3&4\\P(X)&0.1&0.2&0.3&0.25&0.15.\end{array}\right`

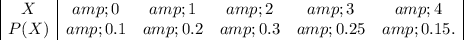
Y = the total number of packages to be wrapped for the customers waiting in line

`\left\begin{array}Y&1&2&3\\P(Y)&0.55&0.35&0.1\end{array}\right|`

a. P(X = 3, Y = 3)

p(3,3) means that there are 3 customers with one gift each

The probability of this event happening:

`0.25 * 0.55^3=0.0416`

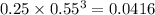
p(3,3)=0.0416

b. p(4,11)

For 4 people to have a total package of 11, there must be 3 customers with 3 packages each and 1 customer with 2 packages,

The probability of this happening is:

`p(4,11)=0.15*^4C_1*0.1^3*0.35\\p(4,11)=0.0002`