Answer:
Explanation:
We will use the reduction of order to solve this equation. At first, we need a solution of the homogeneus solution.
Consider the equation
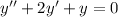 We will assume that the solution is of the form
We will assume that the solution is of the form
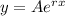 . If we plug this in the equation, we get
. If we plug this in the equation, we get
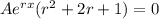
Since the exponential function is a positive function, and A should be different to zero to have non trivial solutions, we get

By using the quadratic formula, we get the solutions
![r= \frac{-2\pm \sqrt[]{4-4}}{2}=-1](https://img.qammunity.org/2021/formulas/mathematics/college/oq9xekiay13g2bjnafy3zymuhu22558re8.png)
So one solution of the homogeneus equation is of the form
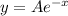 . To use the reduction of order assume that
. To use the reduction of order assume that
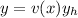
where
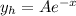 . We calculate the derivatives and plug it in the equation
. We calculate the derivatives and plug it in the equation

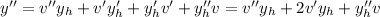
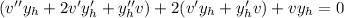
If we rearrange the equation we get
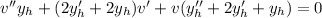
Since
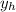 is a solution of the homogeneus equation we get
is a solution of the homogeneus equation we get
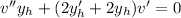
If we take w = v', then w' = v''. So, in this case the equation becomes

Note that
 so
so
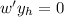 . Since
. Since
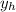 cannot be zero, this implies
cannot be zero, this implies
w' =0. Then, w = K (a constant). Then v' = K. So v=Kx+D where D is a constant.
So, we get that the general solution is
 where C, F are constants.
where C, F are constants.