Answer:
vertex = (0, -4)
equation of the parabola:
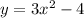
Explanation:
Given:
- y-intercept of parabola: -4
- parabola passes through points: (-2, 8) and (1, -1)
Vertex form of a parabola:
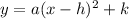
(where (h, k) is the vertex and
 is some constant)
is some constant)
Substitute point (0, -4) into the equation:
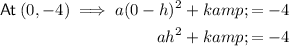
Substitute point (-2, 8) and
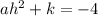 into the equation:
into the equation:
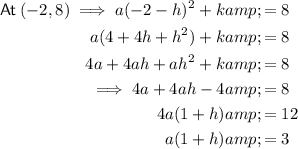
Substitute point (1, -1) and
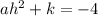 into the equation:
into the equation:
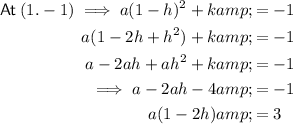
Equate to find h:
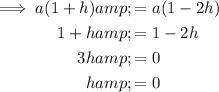
Substitute found value of h into one of the equations to find a:
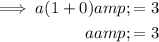
Substitute found values of h and a to find k:
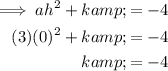
Therefore, the equation of the parabola in vertex form is:
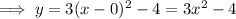
So the vertex of the parabola is (0, -4)