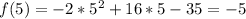Question

Write the quadratic function in the form f(x)=a(x-h)^2+k. Then, give the vertex of its graph. Finally, graph the function by plotting the vertex and four additional points, two on each side of the vertex. f(x)=-2x^2+16x-35

Answer 1

`f(x) = -2(x - 4)^2 -3`

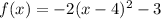
Vertex = (4, -3)

Graph in the image attached, additional points:

(2, -11), (3, -5), (5, -5), (6, -11)

Explanation:

The vertex of f(x) can be found using the formula:

`x_(vertex) = -b/2a`

`x_(vertex) = -16 / (-4)`

`x_(vertex) = 4`

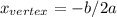
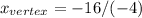
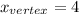
to find y_vertex, we use x_vertex in f(x):

`f(x_(vertex)) = -2 * 4^2 + 16*4 - 35`

`f(x_(vertex)) = -3`

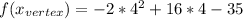
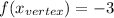
So the vertex is (4, -3)

To write the function in the form
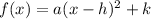`f(x)=a(x-h)^2+k`, we just need to calculate h = -b/2a and then find k:

`h = -b/2a = -16/(-4) = 4`

`f(x) = -2(x - 4)^2 + k = -2(x^2 - 8x + 16) + k = -2x^2 + 16x - 32 + k`

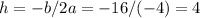
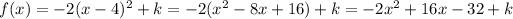
Comparing both forms of f(x), we have:

`-32 + k = -35`

`k = -3`

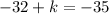
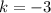
So we have:

`f(x) = -2(x - 4)^2 -3`

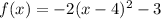
Now let's find the four additional points.

Two points to the left: x = 3 and x = 2

`f(3) = -2 * 3^2 + 16*3 - 35 = -5`

`f(2) = -2 * 2^2 + 16*2 - 35 = -11`

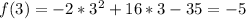
Two points to the right: x = 5 and x = 6

`f(5) = -2 * 5^2 + 16*5 - 35 = -5`

`f(6) = -2 * 6^2 + 16*6 - 35 = -11`