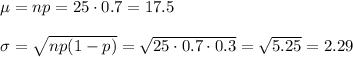Question

PhD’s in Engineering. The National Science Foundation reports that 70% of the U.S. graduate students who earn PhD degrees in engineering are foreign nationals. Consider the number Y of foreign students in a random sample of 25 engineering students who recently earned their PhD.a) Find the probability that there are exactly 10 foreign students in your sample – use equation for thisb) Find the probability that there are less than or equal to 5 foreign students in your sample andc) Find the mean and standard deviation for Y

Answer 1

a) P(Y=10)=0.0013

b) P(Y≤5)=0.00000035

c) Mean = 17.5

S.D. = 2.29

Explanation:

We can model this as a binomial random variable with n=25 and p=0.7.

The probability that k students from the sample are foreign students can be calculated as:

`P(y=k) = \dbinom{n}{k} p^(k)(1-p)^(n-k)\\\\\\P(y=k) = \dbinom{25}{k} 0.7^(k) 0.3^(25-k)\\\\\\`

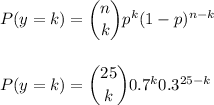
a) Then, for Y=10, the probability is:

`P(y=10) = \dbinom{25}{10} p^(10)(1-p)^(15)=3268760*0.0282475249*0.0000000143\\\\\\P(y=10)=0.0013\\\\\\`

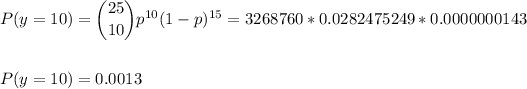
b) We have to calculate the probability P(Y≤5)

`P(y\leq5)=P(Y=0)+P(Y=1)+...+P(Y=5)\\\\\\P(x=0) = \dbinom{25}{0} p^(0)(1-p)^(25)=1*1*0=0\\\\\\P(y=1) = \dbinom{25}{1} p^(1)(1-p)^(24)=25*0.7*0=0\\\\\\P(y=2) = \dbinom{25}{2} p^(2)(1-p)^(23)=300*0.49*0=0.0000000001\\\\\\P(y=3) = \dbinom{25}{3} p^(3)(1-p)^(22)=2300*0.343*0=0.0000000025\\\\\\P(y=4) = \dbinom{25}{4} p^(4)(1-p)^(21)=12650*0.2401*0=0.0000000318\\\\\\P(y=5) = \dbinom{25}{5} p^(5)(1-p)^(20)=53130*0.16807*0=0.0000003114\\\\\\\\`

`P(y\leq5)=0+0+0.0000000001+0.0000000025+0.0000000318+0.00000031\\\\P(y\leq5)= 0.00000035`

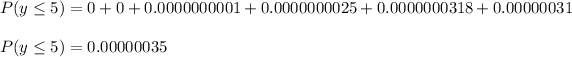
c) The mean and standard deviation for this binomial distribution can be calculated as:

`\mu=np=25\cdot 0.7=17.5\\\\\sigma=√(np(1-p))=√(25\cdot0.7\cdot0.3)=√(5.25)=2.29`