Question

A portfolio has average return of 13.2 percent and standard deviation of returns of 18.9 percent. Assuming that the portfolioi's returns are normally distributed, what is the probability that the portfolio's return in any given year is between -43.5 percent and 32.1 percent?

A. 0.950
B. 0.835
C. 0.815
D. 0.970

Answer 1

B. 0.835

Explanation:

We can use the z-scores and the standard normal distribution to calculate this probability.

We have a normal distribution for the portfolio return, with mean 13.2 and standard deviation 18.9.

We have to calculate the probability that the portfolio's return in any given year is between -43.5 and 32.1.

Then, the z-scores for X=-43.5 and 32.1 are:

`z_1=(X_1-\mu)/(\sigma)=((-43.5)-13.2)/(18.9)=(-56.7)/(18.9)=-3\\\\\\z_2=(X_2-\mu)/(\sigma)=(32.1-13.2)/(18.9)=(18.9)/(18.9)=1\\\\\\`

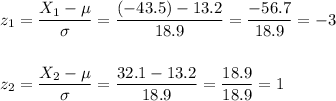
Then, the probability that the portfolio's return in any given year is between -43.5 and 32.1 is:

`P(-43.5<X<32.1)=P(z<1)-P(z<-3)\\\\P(-43.5<X<32.1)=0.841-0.001=0.840`