Answer:
The smallest whole number that can be the value of the expression is 2
Explanation:
Given that the letters represent different digits, to get the smallest whole number value for the expression we have;
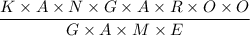
The letters G and A cancel out from the numerator and the denominator to give;
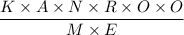
Therefore, the smallest whole number can be from 2 and above as the product of six digits is more than one times the product of two digits
If we put
K = 2, A = 3, N = 4, R = 6, O = 1, M = 9, and E = 8, we have;
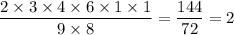
Therefore, the smallest whole number that can be the value of the expression = 2.