Question

Which statement best describes how to determine whether f(x) = 9- 4x4 is an odd function?

Determine whether 9-4(-x)2 is equivalent to 9 - 4x2.
O Determine whether 9 -4(-x?) is equivalent to 9 + 4x².
Determine whether 9 -4(-x)2 is equivalent to -(9 - 4x2).
Determine whether 9 -4(-x?) is equivalent to -19 + 4x?).

Answer 1

Option C.

Explanation:

Note: In the given function the power of x should be 2 instead of 4, otherwise all options are incorrect.

Consider the given function is

`f(x)=9-4x^2`

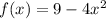
If
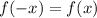`f(-x)=f(x)`, then
`f(x)` is an even function.

If
`f(-x)=-f(x)`, then
`f(x)` is an odd function.

Now, substitute x=-x in the given function.

`f(-x)=9-4(-x)^2`

`f(-x)=9-4(x)^2`

`f(-x)=f(x)`

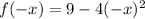
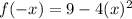
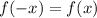
So, the given function not an odd function. It means it is an even function.

To check whether the given function is odd, we have to determine whether
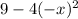`9-4(-x)^2` is equivalent to
`-(9-4(x)^2)`.

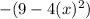Therefore, the correct option is C.