Question

Couldddddddddd i have some help super fast?

Answer 1

`\textsf{a)} \quad P=-20(x-2)^2+3380`

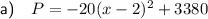
b) cost of ticket = $13

max profit = $3380

number of tickets sold = 260

Explanation:

Profit equation:
`P=20(15-x)(11+x)`

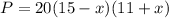
Part (a)

Vertex form of quadratic equation:
`y=a(x-h)^2+k`

(where (h, k) is the vertex and
`a` is some constant)

First, write the given profit equation in standard form
`ax^2+bx+c`:

`\begin{aligned}\implies P&=20(15-x)(11+x)\\& = 20(165+4x-x^2)\\& = -20x^2+80x+3300\end{aligned}`

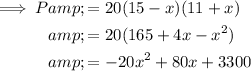
Factor -20 from the first two terms:

`\implies P=-20(x^2-4x)+3300`

Complete the square:

`\implies P=-20(x^2-4x+4)+80+3300`

`\implies P=-20(x-2)^2+3380`

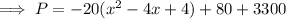
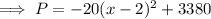
Part (b)

The vertex of the profit equation is (2, 3380).

Therefore, the cost of the ticket is when x = 2 ⇒ $11 + 2 = $13

The maximum profit is the y-value of the vertex: $3380

The number of tickets sold at this price is:

⇒ max profit ÷ ticket price

= 3380 ÷ 13

= 260