Answer:
(a)
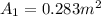
(b)
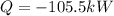 : From the air to the surroundings.
: From the air to the surroundings.
Step-by-step explanation:
Hello,
(a) In this case, we can compute the area at the entrance by firstly computing the inlet volumetric flow:
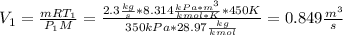
Then, with the velocity, we compute the area:

(b) In this case, via the following energy balance for the nozzle:
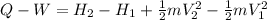
We can easily compute the change in the enthalpy by using the given Cp and neglecting the work (no done work):
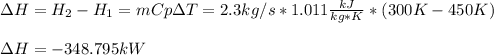
Finally, the heat turns out:
![Q=-348.795kW+(1)/(2)*2.3(kg)/(s)*[(460(m)/(s))^2 -(3(m)/(s))^2 ]\\\\Q=-348.795kW+243329.65W*(1kW)/(1000W)\\ \\Q=-105.5kW](https://img.qammunity.org/2021/formulas/physics/college/34euxgmo3vmrzdwcqfpd56dgdvy58homk2.png)
Such sign, means the heat is being transferred from the air to the surroundings.
Regards.