Question

25) The endpoints of the diameter of a circle are (6, 5) and (−2, 3). Which equation represents the circle? A) (x − 2)2 + (y − 4)2 = 9 B) ( x+ 2)2 + (y + 4)2 = 16 C) (x − 2)2 − (y + 4)2 = 16 D) (x − 2)2 + (y − 4)2 = 17

Answer 1

Option D.

Explanation:

It is given that the endpoints of the diameter of a circle are (6, 5) and (−2, 3). So, midpoint of these end point is the center of the circle.

`Center=\left((x_1+x_2)/(2),(y_1+y_2)/(2)\right)`

`Center=\left((6+(-2))/(2),(5+3)/(2)\right)`

`Center=\left((4)/(2),(8)/(2)\right)`

`Center=\left(2,4\right)`

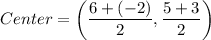
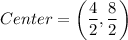
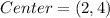
So, center of the circle is (2,4).

Length of diameter of the circle is the distance between (6, 5) and (−2, 3).

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

`d=√((-2-6)^2+(3-5)^2)`

`d=√((-8)^2+(-2)^2)`

`d=√(64+4)`

`d=√(68)`

`d=2√(17)`

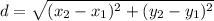
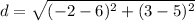
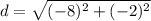
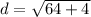
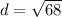
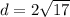
So, radius of the circle is

`r=(d)/(2)=(2√(17))/(2)=√(17)`

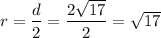
Standard form of a circle is

`(x-h)^2+(y-k)^2=r^2`

where, (h,k) is center of the circle and r is radius.

Substitute h=2, k=4 and
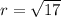`r=√(17)` in the above equation.

`(x-2)^2+(y-4)^2=(√(17))^2`

`(x-2)^2+(y-4)^2=17`

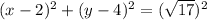
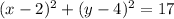
Therefore, the correct option is D.