Question

You throw a ball straight up into the air from the top of a building. The building has a height of 15.0 m. The ball reaches a height (measured from the ground) of 25.0 m and then it starts to fall back down.

a) Determine the initial velocity of the ball.
b) What is the velocity of the ball when it comes back down and is at the same height from which it was thrown?
c) How long will it take the ball to come back down to this height from the time at which it was first thrown?
d) Let’s say that you missed catching the ball on the way back down and it fell to the ground. How long did it take to hit the ground from the moment you threw it up?
e) What was the ball’s final velocity the moment before it hit the ground?

Answer 1

a) vo = 14m/s

b) v = 14m/s

c) t = 2.85s

d) t = 0.829s

e) v = 22.12 m/s

Step-by-step explanation:

a) To find the initial velocity of the ball yo use the following formula:

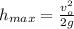`h_(max)=(v_o^2)/(2g)` (1)

hmax: maximum height reached by the ball but measured from the point at which the ball is thrown = 25.0m - 15.0m = 10.0m

vo: initial velocity of the ball = ?

g: gravitational acceleration = 9.8m/s^2

You solve the equation (1) for vo and replace the values of the other parameters:

`v_o=\sqrt{2gh_(max)}}=√(2(9.8m/s^2)(10.0m))=14(m)/(s)`

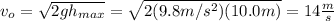
The initial velocity of the ball is 14m/s

b) To find the velocity of the ball when it is at the same position as the initial point where it was thrown, you can use the following formula:

`v^2=2gh_(max)\\\\v=\sqrt{2gh_(max)}`

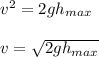
as you can notice, v = vo = 14m/s

The velocity of the ball is 14 m/s

c) The flight time of the ball is given by twice the time the ball takes to reach the maximum height. You use the following formula:

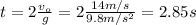`t=2(v_o)/(g)=2(14m/s)/(9.8m/s^2)=2.85s` (3)

The time is 2.85s

d) To find the time the ball takes to arrive to the ground after the ball passes the same height at which is was thrown, you can use the following formula:

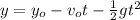`y=y_o-v_ot-(1)/(2)gt^2` (4)

y: 0 m (ball just after it impact the ground)

yo: initial position = 15.0 m

vo: in)itial velocity of the ball = 14m/s

t: time

You replace the values of the parameters in the equation (4) and obtain a quadratic formula:

`0=15.0-14t-(1)/(2)(9.8)t^2\\\\`

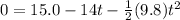
You use the quadratic formula to find the roots t:

`t_(1,2)=(-(-14)\pm√((-14)^2-4(4.9)(15)))/(2(-4.9))\\\\t_(1,2)=(14\pm22.13)/(-9.8)\\\\t_1=0.829s\\\\t_2=-2.19s`

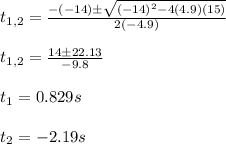
you choose the positive values because is has physical meaning

The time the ball takes to arrive to the ground is 0.829s

e) The final velocity is:

`v=v_o+gt`

`v=14m/s+(9.8m/s^2)(0.829s)=22.12(m)/(s)`

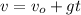
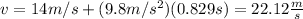
The final velocity is 22.14 m/s