Question

A 50-kg block is pushed a distance of 5.0 m across a floor by a horizontal force Fp whose magnitude is 150 N. Fp is parallel to the displacement of the block. The coefficient of kinetic friction is 0.25.

a) What is the total work done on the block?
b) If the box started from rest, what is the final speed of the block?

Answer 1

a) WT = 137.5 J

b) v2 = 2.34 m/s

Step-by-step explanation:

a) The total work done on the block is given by the following formula:

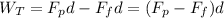`W_T=F_pd-F_fd=(F_p-F_f)d` (1)

Fp: force parallel to the displacement of the block = 150N

Ff: friction force

d: distance = 5.0 m

Then, you first calculate the friction force by using the following relation:

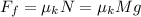`F_f=\mu_k N=\mu_k Mg` (2)

μk: coefficient of kinetic friction = 0.25

M: mass of the block = 50kg

g: gravitational constant = 9.8 m/s^2

Next, you replace the equation (2) into the equation (1) and solve for WT:

`W_T=(F_p-\mu_kMg)d=(150N-(0.25)(50kg)(9.8m/s^2))(5.0m)\\\\W_T=137.5J`

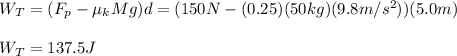
The work done over the block is 137.5 J

b) If the block started from rest, you can use the following equation to calculate the final speed of the block:

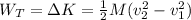`W_T=\Delta K=(1)/(2)M(v_2^2-v_1^2)` (3)

WT: total work = 137.5 J

v2: final speed = ?

v1: initial speed of the block = 0m/s

You solve the equation (3) for v2:

`v_2=\sqrt{(2W_T)/(M)}=\sqrt{(2(137.5J))/(50kg)}=2.34(m)/(s)`

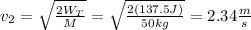
The final speed of the block is 2.34 m/s