Answer: The mass of the silver block is 256 grams
Step-by-step explanation:
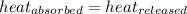
As we know that,
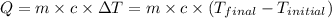
![m_1* c_1* (T_(final)-T_1)=-[m_2* c_2* (T_(final)-T_2)]](https://img.qammunity.org/2021/formulas/chemistry/college/8mq914tycmkoswztk5p5my04anxw73dmzg.png) .................(1)
.................(1)
where,
q = heat absorbed or released
 = mass of silver = ?
= mass of silver = ?
 = mass of water = 100.0 g
= mass of water = 100.0 g
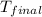 = final temperature =
= final temperature =
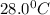
 = temperature of silver =
= temperature of silver =
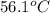
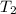 = temperature of water =
= temperature of water =

 = specific heat of silver =
= specific heat of silver =

 = specific heat of water=
= specific heat of water=
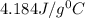
Now put all the given values in equation (1), we get
![-m_1* 0.233* (28.0-56.1)=[100.0* 4.184* (28.0-24.0)]](https://img.qammunity.org/2021/formulas/chemistry/college/yvrrmzbbh7m43lffm3pdkdcryc2h8hqslu.png)
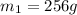
Therefore, the mass of the silver block is 256 grams