Question

Kelly has $800, which she divides between two savings accounts. One account earns 2% simple interest and the other earns 5%. If she earns $31 in interest between the two accounts, how much is in each?

Answer 1

On the first account, she invests $300, earning 0.02*300 = $6.

On the second acount, she invests 800 - 300 = $500, earning $25.

Explanation:

This is a simple interest problem.

The simple interest formula is given by:

`E = P*I*t`

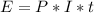
In which E is the amount of interest earned, P is the principal(the initial amount of money), I is the interest rate(yearly, as a decimal) and t is the time.

In this question:

Two acounts, one with 2% interest(I = 0.02) and the other with 5% interest(I = 0.05).

Each account has two earnings, that i will call
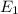`E_(1)` and
`E_(2)`

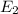
Two investments adding up to 800. I will call the first investment P and the second is 800 - P.

Time is not given, but for simplicity, i will use 1 year.

First investment:

I at 2%. The earnings are
`E_(1)`.

`E_(1) = 0.02P`

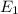Second Investment:

Earnings
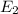`E_(2)`, at 5%. So

`E_(2) = 0.05(800 - P)`

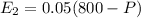
The earnings add to 31, so
`E_(1) + E_(2) = 31`, then

`E_(2) = 31 - E_(1)`

So

`31 - E_(1) = 0.05(800 - P)`

`31 - 0.02P = 0.05(800 - P)`

`31 - 0.02P = 40 - 0.05P`

`0.03P = 9`

`P = (9)/(0.03)`

`P = 300`

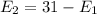
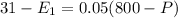
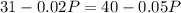
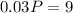
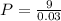
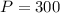
So:

On the first account, she invests $300, earning 0.02*300 = $6.

On the second acount, she invests 800 - 300 = $500, earning $25.