Question

A line segment has endpoints at (4.-6) and (0,2).

What is the slope of the given line segment?
What is the midpoint of the given line segment?
What is the slope of the perpendicular bisector of the given line segment?
What is the equation, in slope-intercept form, of the perpendicular bisector?

Answer 1

see explanation

Explanation:

Calculate the slope m using the slope formula

m =
`(y_(2)-y_(1) )/(x_(2)-x_(1) )`

with (x₁, y₁ ) = (4, - 6) and (x₂, y₂ ) = (0, 2)

m =
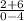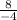`(2+6)/(0-4)` =
`(8)/(-4)` = - 2

---------------------------------------

Find the midpoint using the midpoint formula

M =(
`(x_(1)+x_(2) )/(2)` ,
`(y_(1)+y_(2) )/(2)` )

=
`(4+0)/(2)` ,
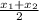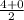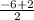`(-6+2)/(2)` ) = (2, - 2 )

-----------------------------------------------

Given a line with slope m then the slope of a line perpendicular to it is

`m_(perpendicular)` = -
`(1)/(m)` = -
`(1)/(-2)` =
`(1)/(2)`

----------------------------------------------

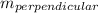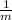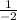The equation of a line in slope- intercept form is

y = mx + c ( m is the slope and c the y- intercept )

Here m =
`(1)/(2)` , thus

y =
`(1)/(2)` x + c ← is the partial equation

To find c substitute (2, - 2) into the partial equation

- 2 = 1 + c ⇒ c = - 2 - 1 = - 3

y =
`(1)/(2)` x - 3 ← equation of perpendicular bisector

Answer 2

• -2
• (2, -2)
• 1/2
• y= 1/2x - 3

Explanation:

Points given: (4, -6) and (0, 2)

Slope intercept form of the line going through the given pints:

y= mx+b

• m= (y2-y1)/(x2-x1)= (2+6)/(0-4)= -2 slope is -2

y= -2x+b ⇒ -6= -2*4+b ⇒ b= 8-6= 2 ⇒ y= -2x+2

• Mid point= (x1+x2)/2, (y1+y2)/2= (4+0)/2, (-6+2)/2= (2, -2)

The slope of the perpendicular bisector is the negative reciprocal of the line segment which it is dividing:

• m'= -1/m= -1/-2= 1/2

Equation of perpendicular bisector:

• y= 1/2x+b

It passes through the mid point: (2, -2), so

• b= y - 1/2x= -2 - 1/2*2= -2 -1= -3

So the equation of perpendicular line:

• y= 1/2x - 3