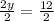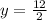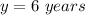Answer:
6 years
Step-by-step explanation:
The subject Mathematics (not Spanish); however, the solution is as follows...
Given
Height of Type A: 7ft
Growth of Type A = 11in per year
Height of Type B: 8ft
Growth of Type B = 9in per year
Required
When both trees would have the same height
First, the units of height and growth of both trees must be the same.
So, we'll convert the height from feet to inches
Given that 1 foot = 12 inches
Height of Type A: 7 * 12 inches = 84 inches
Height of Type B: 8 * 12 inches = 96 inches
Let y represent the number of years, both trees would have the same height
Type A can be represented algebraically as : 84 + 11y
Type B can be represented algebraically as : 96 + 9y
To solve further, we have to equate both expressions
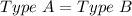
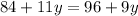
Collect Like Terms
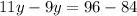

Divide both sides by 2