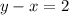Answer:
Explanation:
Given
Points (-2,0) and (-3,-1)
Required
Equation of Line
The first step is to determine the slope of the line; using the following formula


 becomes
becomes

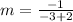
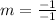
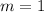
The next is to determine the equation of the line using any of the points
The formula is as thus;
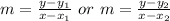
Using

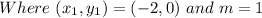
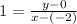
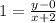
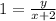
Multiply both sides by x + 2
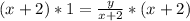
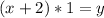
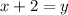
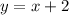
Subtract x from both sides
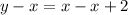
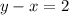
Hence, the equation of the line in standard form is