Answer:
D: 9
Step-by-Step Explanation:
The average rate is synonymous with the slope. Since we want to find the average rate of change from x = 5 to x = 6, we will use the two points (5, 18) and (6, ?). We will need to find ? first.
Since the table represents a quadratic function and we are given the vertex, we can use the vertex form of a quadratic:
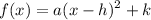
Where (h, k) is the vertex.
The vertex is (1, 2). Hence:
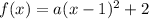
To determine a, pick a sample point from the table and solve for a. We can use (2, 3). Hence:
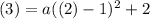
Solve for a:
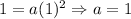
Hence, our function is:
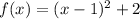
Evaluate the function when x = 6:
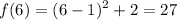
So, our two points are (5, 18) and (6, 27).
Again, to find the average rate of change between x= 5 and x = 6, find the slope between their two points. Hence:
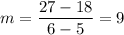
Our answer is D.