Question

Suppose a triangle has two sides of length 32 and 35, and that the angle

between these two sides is 120°. What is the length of the third side of the
triangle?

Answer 1

In the picture below

Answer 2

The third side is around 58.04 units.

Explanation:

Since we are given two sides and the angle between the two sides, and we want to find the third side, we can use the law of cosines. The law of cosines is given by:

`\displaystyle c^2=a^2+b^2-2ab\cos(C)`

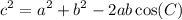
Where a and b are the two side lengths adjacent to the angle C and c is the third side length.

Substitute:

`c^2=32^2+35^2-2(32)(35)\cos(120)`

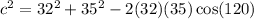
Solve for c:

`c=√(32^2+35^2-2(32)(35)\cos(120))`

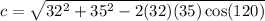
Evaluate using a calculator:

`c\approx 58.04\text{ units}`

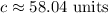
The third side is around 58.04 units.