Question

A 72-kg skydiver is falling from 10000 feet. At an instant during the fall, the skydiver

encounters an air resistance force of 540 Newtons. The acceleration of the skydiver at
this instant is
m/s2

Answer 1

Approximately
`2.31\; \rm m \cdot s^(-2)` (assuming that the acceleration due to gravity is
`g = 9.81\; \rm m \cdot s^(-2)`.)

Step-by-step explanation:

Assuming that
`g = 9.81\; \rm m \cdot s^(-2)` the weight on this 72-kg skydiver would be
`W = m \cdot g = 72 \; \rm kg * 9.81\; \rm m \cdot s^(-2) = 706.32\; \rm N` (points downwards.)

Air resistance is supposed to act in the opposite direction of the motion. Since this skydiver is moving downwards, the air resistance on the skydiver would point upwards.

Therefore, the net force on this skydiver should be the difference between the weight and the air resistance on the skydiver:

`\begin{aligned}F(\text{net force}) &= W - F(\text{air resistance})\\ &= 706.32\; \rm N - 540\; \rm N =166.32\; \rm N \end{aligned}`.

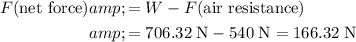Apply Newton's Second Law of motion to find the acceleration of this skydiver:

`\begin{aligned}a &= \frac{F(\text{net force})}{m} \\ &= (166.32\; \rm N)/(72\; \rm kg) = 2.31\; \rm m \cdot s^(-2) \end{aligned}`.