Question

Use a graph to find the range of the function f(x) = 5/x^2
on the domain -5 < x < 5.

Answer 1

Option A.

Explanation:

The given function is

`f(x)=(5)/(x^2)`

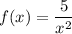
We need to find the range of the function f(x) on the domain
`-5\leq x\leq 5`.

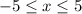At x=-5,

`f(-5)=(5)/((-5)^2)=(5)/(25)=(1)/(5)`

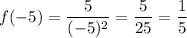
At x=5,

`f(5)=(5)/((5)^2)=(5)/(25)=(1)/(5)`

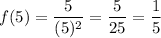
As x approaches to 0, then the function approaches to positive infinity.

Draw the graph of given function as shown below.

In the graph x-axis represents the domain and y-axis represents the range.

From the graph it is clear that on the domain
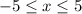`-5\leq x\leq 5` the value of function is greater than or equal to
`(1)/(5)`.

So, range is
`f(x)\geq (1)/(5).`

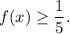
Therefore, the correct option is A.